 |
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Sparsifying MCA with exponential
Up: Seislet-based MCA sparsified with
Previous: Seislet-based MCA sparsified with
Seislet transform and seislet frame were proposed by Fomel and Liu (2010) for seismic data compression and sparse representation. Seislets are constructed by applying the wavelet lifting scheme (Sweldens, 1998) along the local slope direction. For each level of lifting decomposition, seismic data is split into even and odd parts (
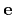 and
and
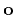 ). Then the prediction and update step follows to obtain the detail difference/residual
). Then the prediction and update step follows to obtain the detail difference/residual
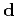 and smooth information
and smooth information
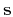 :
:
![$\displaystyle \mathbf{d}=\mathbf{e}-P[\mathbf{o}],\mathbf{s}=\mathbf{e}+U[\mathbf{d}].$](img61.png) |
(15) |
Recognizing that seismic data can be organized as collections of traces or records, Fomel and Liu (2010) suggest prediction of one seismic trace or record from its neighbors and update of records on the next scale to follow structural features in seismic data. In the 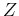 -transform notation, the simplest Haar prediction filter can be written as
-transform notation, the simplest Haar prediction filter can be written as
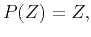 |
(16) |
and the linear interpolation prediction filter is
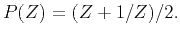 |
(17) |
Successful prediction and update play a key role for local slope estimation. By modifying the biorthogonal wavelet construction, the prediction and update operators for a simple seislet transform are defined as
![\begin{displaymath}\begin{split}P[\mathbf{e}]_k=(S_k^{+}[\mathbf{e}_{k-1}] + S_{...
...}[\mathbf{r}_{k-1}] + S_{k}^{-} [\mathbf{r}_k]) /4, \end{split}\end{displaymath}](img65.png) |
(18) |
where 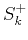 and
and 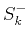 are the operators that predict a trace from its left and right neighbors, corresponding to shifting seismic events in terms of their local slopes. The job of local slope estimation can be done by PWD filters. Particularly, it is possible to obtain two or more dips with the help of PWD filters to capture different geometrical components of seismic data. The estimation of slopes involves a least-square optimization problem to be solved (Fomel, 2002), leading to extra computation. It is important to point out that besides PWD, there are other approaches to estimating dips of seismic data, i.e., local slant stack (Ottolini, 1983) and volumetric scan (Marfurt, 2006). However, PWD implements slope estimation through prediction and therefore is appropriate for use with the seislet transform.
are the operators that predict a trace from its left and right neighbors, corresponding to shifting seismic events in terms of their local slopes. The job of local slope estimation can be done by PWD filters. Particularly, it is possible to obtain two or more dips with the help of PWD filters to capture different geometrical components of seismic data. The estimation of slopes involves a least-square optimization problem to be solved (Fomel, 2002), leading to extra computation. It is important to point out that besides PWD, there are other approaches to estimating dips of seismic data, i.e., local slant stack (Ottolini, 1983) and volumetric scan (Marfurt, 2006). However, PWD implements slope estimation through prediction and therefore is appropriate for use with the seislet transform.
 |
 |
 |
 | Seislet-based morphological component analysis using scale-dependent exponential shrinkage |  |
![[pdf]](icons/pdf.png) |
Next: Sparsifying MCA with exponential
Up: Seislet-based MCA sparsified with
Previous: Seislet-based MCA sparsified with
2021-08-31
![]() and
and
![]() ). Then the prediction and update step follows to obtain the detail difference/residual
). Then the prediction and update step follows to obtain the detail difference/residual
![]() and smooth information
and smooth information
![]() :
:
![\begin{displaymath}\begin{split}P[\mathbf{e}]_k=(S_k^{+}[\mathbf{e}_{k-1}] + S_{...
...}[\mathbf{r}_{k-1}] + S_{k}^{-} [\mathbf{r}_k]) /4, \end{split}\end{displaymath}](img65.png)