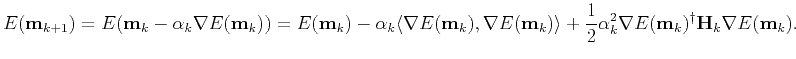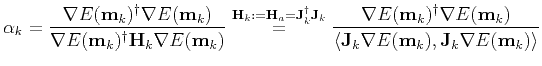A numerical tour of wave propagation

The Newton, Gauss-Newton, and steepest-descent methods

In terms of Eq. (64),

$$\begin{split}\frac{\partial E(\textbf{m})}{\partial m_i} &=\f... ...^{\dagger}\Delta \textbf{p}\right], i=1,2,\ldots,M. \end{split}$$ (71)

That is to say,

$$\nabla E_{\textbf{m}}=\nabla E(\textbf{m})=\frac{\partial E(\text... ...textbf{p}\right] =\mathtt{Re}\left[\textbf{J}^{\dagger}\Delta \textbf{p}\right]$$ (72)

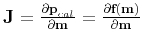where $\mathtt{Re}$ takes the real part, and $\textbf{J}=\frac{\partial \textbf{p}_{cal}}{\partial \textbf{m}}=\frac{\partial \textbf{f}(\textbf{m})}{\partial \textbf{m}}$ is the Jacobian matrix, i.e., the sensitivity or the Fréchet derivative matrix.

Differentiation of the gradient expression (71) with respect to the model parameters gives the following expression for the Hessian 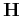$\textbf{H}$ :

$$\begin{split}\textbf{H}_{i,j}&=\frac{\partial^2 E(\textbf{m})... ...frac{\partial\textbf{p}_{cal}}{\partial m_j}\right] \end{split}$$ (73)

In matrix form

$$\textbf{H}=\frac{\partial^2 E(\textbf{m})}{\partial \textbf{m}^2}... ...(\Delta \textbf{p}^*, \Delta \textbf{p}^*, \ldots, \Delta \textbf{p}^*)\right].$$ (74)

In many cases, this second-order term is neglected for nonlinear inverse problems. In the following, the remaining term in the Hessian, i.e., $\textbf{H}_a=\mathtt{Re}[\textbf{J}^{\dagger}\textbf{J}]$ , is referred to as the approximate Hessian. It is the auto-correlation of the derivative wavefield. Eq. (68) becomes

$$\Delta \textbf{m} =-\textbf{H}^{-1}\nabla E_{\textbf{m}} =-\textbf{H}_a^{-1}\mathtt{Re}[\textbf{J}^{\dagger}\Delta \textbf{p}].$$ (75)

The method which solves equation (74) when only 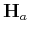$\textbf{H}_a$ is estimated is referred to as the Gauss-Newton method. To guarantee th stability of the algorithm (avoiding the singularity), we can use 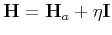$\textbf{H}=\textbf{H}_a+\eta \textbf{I}$ , leading to

$$\Delta \textbf{m} =-\textbf{H}^{-1}\nabla E_{\textbf{m}} =-(\text... ... \textbf{I})^{-1}\mathtt{Re}\left[\textbf{J}^{\dagger}\Delta \textbf{p}\right].$$ (76)

Alternatively, the inverse of the Hessian in Eq. (68) can be replaced by 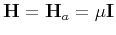$\textbf{H}=\textbf{H}_a=\mu \textbf{I}$ , leading to the gradient or steepest-descent method:

$$\Delta \textbf{m} =-\mu^{-1}\nabla E_{\textbf{m}} =-\alpha\nabla ... ...a\mathtt{Re}\left[\textbf{J}^{\dagger}\Delta \textbf{p}\right],\alpha=\mu^{-1}.$$ (77)

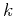At the $k$ -th iteration, the misfit function can be presented using the 2nd-order Taylor-Lagrange expansion

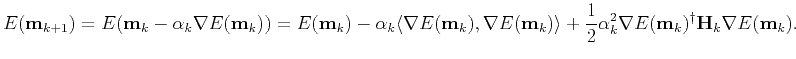$$E(\textbf{m}_{k+1})=E(\textbf{m}_k-\alpha_k \nabla E(\textbf{m}_k... ...2}\alpha_k^2\nabla E(\textbf{m}_k)^{\dagger}\textbf{H}_k\nabla E(\textbf{m}_k).$$ (78)

Setting $\frac{\partial E(\textbf{m}_{k+1})}{\partial \alpha_k}=0$ gives

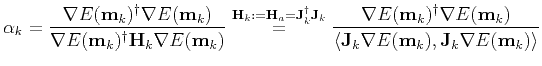$$\alpha_k=\frac{\nabla E(\textbf{m}_k)^{\dagger}\nabla E(\textbf{m... ...le\textbf{J}_k\nabla E(\textbf{m}_k),\textbf{J}_k\nabla E(\textbf{m}_k)\rangle}$$ (79)

A numerical tour of wave propagation