 |
 |
 |
 | Noncausal  -
- -
-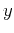 regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data
regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data |  |
![[pdf]](icons/pdf.png) |
Next: f-x-y NRNA for random
Up: Methodology
Previous: Methodology
Seismic section 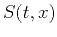 in
in  -
- domain is predictable if it only
includes linear events in
domain is predictable if it only
includes linear events in 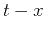 domain. The relationship between the
n-th trace and (n-i)-th trace can be easily described as
domain. The relationship between the
n-th trace and (n-i)-th trace can be easily described as
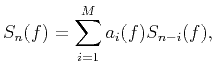 |
(1) |
where M is the number of events in 2D seismic section. Eq. (1) describes
forward prediction equations, namely causal prediction filtering equations
(Gulunay, 2000). In the case of both forward and backward prediction equations
(noncausal prediction filter), Eq. 1 can be written as (Spitz, 1991; Gulunay, 2000; Naghizadeh and Sacchi, 2009; Liu et al., 1991)
where M is the parameter related to the number of events. Note that Eq. 2
implies the assumption
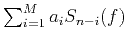 =0
=0 5
5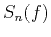 and
and
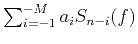 =0
=0 5
5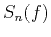 . Theoretically,
. Theoretically, 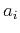 in forward prediction equations
is the complex conjugation of
in forward prediction equations
is the complex conjugation of
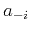 in backward equations (Galbraith, 1984).
Gulunay (2000) pointed that it is possible to reduce the order of the normal equations
from 2M to M because the coefficients of noncausal prediction filter have conjugate symmetry.
f-x prediction filtering has the assumption that the events of seismic section are
linear. If seismic events are not linear, or the amplitudes of wavelet are varying,
they no longer follow linear or stationary assumptions (Canales, 1984). One needs to
perform
in backward equations (Galbraith, 1984).
Gulunay (2000) pointed that it is possible to reduce the order of the normal equations
from 2M to M because the coefficients of noncausal prediction filter have conjugate symmetry.
f-x prediction filtering has the assumption that the events of seismic section are
linear. If seismic events are not linear, or the amplitudes of wavelet are varying,
they no longer follow linear or stationary assumptions (Canales, 1984). One needs to
perform  -
- prediction filtering over a short sliding window in time and space to
cope with continuous changes in dips (Naghizadeh and Sacchi, 2009). Fomel (2009)
developed a general method of RNA using shaping regularization technology, which
is implemented for real number. Liu et al. (1991) extended the RNA method to
prediction filtering over a short sliding window in time and space to
cope with continuous changes in dips (Naghizadeh and Sacchi, 2009). Fomel (2009)
developed a general method of RNA using shaping regularization technology, which
is implemented for real number. Liu et al. (1991) extended the RNA method to  -
- domain for complex numbers and applied it to seismic random noise attenuation for
2D seismic data. The
domain for complex numbers and applied it to seismic random noise attenuation for
2D seismic data. The  -
- NRNA is defined as (Liu et al., 1991)
NRNA is defined as (Liu et al., 1991)
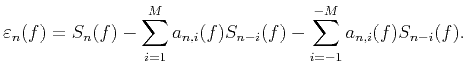 |
(3) |
Eq. 3 indicates that one trace noise-free in  -
- domain can be predicted by
adjacent traces with the different weights
domain can be predicted by
adjacent traces with the different weights
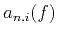 . Note that the
weights
. Note that the
weights
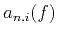 is varying along the space direction, which
indicated by subscript i in
is varying along the space direction, which
indicated by subscript i in
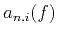 . In Eq. 3, the coefficients
. In Eq. 3, the coefficients 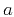 is
the function of space i, but it is not in Eq. 2. When applying
is
the function of space i, but it is not in Eq. 2. When applying  -
- NRNA to seismic
noise attenuation, we assume the prediction error
NRNA to seismic
noise attenuation, we assume the prediction error
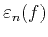 is the
random noise and the predictable part
is the
random noise and the predictable part
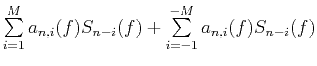 is the signal. Finding spatial-varying coefficients
is the signal. Finding spatial-varying coefficients
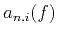 form Eq. 3
is ill-posed problem because there are more unknown variables than constraint equations. To obtain the
coefficients, we should add constraint equations. Shaping regularization (Fomel, 2009)
can be used to solve the under-constrained problem (Liu et al., 1991). The RNA method
can also be used for seismic data processing in t-x-y domain, such as seismic data
interpolation (Liu and Fomel, 2011).
form Eq. 3
is ill-posed problem because there are more unknown variables than constraint equations. To obtain the
coefficients, we should add constraint equations. Shaping regularization (Fomel, 2009)
can be used to solve the under-constrained problem (Liu et al., 1991). The RNA method
can also be used for seismic data processing in t-x-y domain, such as seismic data
interpolation (Liu and Fomel, 2011).
 |
 |
 |
 | Noncausal  -
- -
- regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data
regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data |  |
![[pdf]](icons/pdf.png) |
Next: f-x-y NRNA for random
Up: Methodology
Previous: Methodology
2013-11-13
![]() in
in ![]() -
-![]() domain is predictable if it only
includes linear events in
domain is predictable if it only
includes linear events in ![]() domain. The relationship between the
n-th trace and (n-i)-th trace can be easily described as
domain. The relationship between the
n-th trace and (n-i)-th trace can be easily described as
![]() -
-![]() domain can be predicted by
adjacent traces with the different weights
domain can be predicted by
adjacent traces with the different weights
![]() . Note that the
weights
. Note that the
weights
![]() is varying along the space direction, which
indicated by subscript i in
is varying along the space direction, which
indicated by subscript i in
![]() . In Eq. 3, the coefficients
. In Eq. 3, the coefficients ![]() is
the function of space i, but it is not in Eq. 2. When applying
is
the function of space i, but it is not in Eq. 2. When applying ![]() -
-![]() NRNA to seismic
noise attenuation, we assume the prediction error
NRNA to seismic
noise attenuation, we assume the prediction error
![]() is the
random noise and the predictable part
is the
random noise and the predictable part
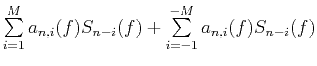 is the signal. Finding spatial-varying coefficients
is the signal. Finding spatial-varying coefficients
![]() form Eq. 3
is ill-posed problem because there are more unknown variables than constraint equations. To obtain the
coefficients, we should add constraint equations. Shaping regularization (Fomel, 2009)
can be used to solve the under-constrained problem (Liu et al., 1991). The RNA method
can also be used for seismic data processing in t-x-y domain, such as seismic data
interpolation (Liu and Fomel, 2011).
form Eq. 3
is ill-posed problem because there are more unknown variables than constraint equations. To obtain the
coefficients, we should add constraint equations. Shaping regularization (Fomel, 2009)
can be used to solve the under-constrained problem (Liu et al., 1991). The RNA method
can also be used for seismic data processing in t-x-y domain, such as seismic data
interpolation (Liu and Fomel, 2011).