 |
 |
 |
 | Wide-azimuth angle gathers for wave-equation migration |  |
![[pdf]](icons/pdf.png) |
Next: Angle decomposition
Up: Sava & Vlad: wide-azimuth
Previous: Imaging conditions
In this section, we derive the formula for the moveout function
characterizing reflections in the extended
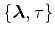 domain. The
purpose of this derivation is to find a procedure for angle
decomposition, i.e. a representation of reflectivity as a function of
reflection and azimuth angles.
domain. The
purpose of this derivation is to find a procedure for angle
decomposition, i.e. a representation of reflectivity as a function of
reflection and azimuth angles.
An implicit assumption made by all methods of angle decomposition is
that we can describe the reflection process by locally planar
objects. Such methods assume that (locally) the reflector is a plane,
and that the incident and reflected wavefields are also (locally)
planar. Only with these assumptions we can define vectors in-between
which we measure angles like the angles of incidence and reflection,
as well as the azimuth angle of the reflection plane. Our method uses
this assumption explicitly.
However, we do not assume that the wavefronts are planar. Instead, we
consider each (complex) wavefront as a superposition of planes with
different orientations. In the following, we discuss how each one of
these planes would behave during the extended imaging and angle
decomposition. Thus, our method applies equally well for simple and
complex wavefields characterized by multipathing.
We define the following unit vectors to describe the reflection
geometry and the conventional and extended imaging conditions:
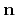 : a unit vector aligned with the reflector normal;
: a unit vector aligned with the reflector normal;
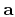 : a unit vector representing the projection of the azimuth
vector
: a unit vector representing the projection of the azimuth
vector 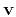 in the reflector plane;
in the reflector plane;
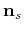 : a unit vector orthogonal to the source wavefront;
: a unit vector orthogonal to the source wavefront;
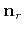 : a unit vector orthogonal to the receiver wavefront;
: a unit vector orthogonal to the receiver wavefront;
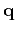 : a unit vector at the intersection of the reflection
plane and the reflector plane.
: a unit vector at the intersection of the reflection
plane and the reflector plane.
By construction, vectors 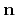 ,
, 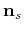 ,
, 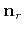 and
and 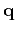 are co-planar
and vectors
are co-planar
and vectors 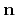 and
and 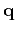 are orthogonal, Figure 1.
are orthogonal, Figure 1.
With these definitions, the (planar) source and receiver wavefields
are given by the expressions:
Here, 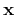 are space coordinates,
are space coordinates, 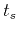 and
and 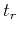 are times defining
the planes under consideration, and
are times defining
the planes under consideration, and 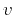 represents velocity.
Equations 6 and 7 define the conventional imaging
condition given by equations 1 and 2. This condition states
that an image is formed when the source and receiver wavefields are
time-coincident at reflection points. In Equations 6 and
7, we explicitly impose the condition that the source and
receiver planes and the reflector plane intersect at the image point.
represents velocity.
Equations 6 and 7 define the conventional imaging
condition given by equations 1 and 2. This condition states
that an image is formed when the source and receiver wavefields are
time-coincident at reflection points. In Equations 6 and
7, we explicitly impose the condition that the source and
receiver planes and the reflector plane intersect at the image point.
Similarly, we can rewrite the extended imaging condition using the
planar approximation of the source and receiver wavefields using the
expressions:
As discussed earlier,
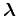 and
and 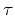 are space- and time-lags, and
are space- and time-lags, and
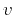 represents the local velocity at the image point, assumed to be
constant in the immediate vicinity of this point. This assumption is
justified by the need to operate with planar objects, as indicated
earlier. With this construction, the source and receiver planes are
shifted relative to one-another by equal quantities in the positive
and negative directions and in space and time, equations 3-4.
represents the local velocity at the image point, assumed to be
constant in the immediate vicinity of this point. This assumption is
justified by the need to operate with planar objects, as indicated
earlier. With this construction, the source and receiver planes are
shifted relative to one-another by equal quantities in the positive
and negative directions and in space and time, equations 3-4.
We can eliminate the space variable 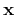 by substituting equation 6
in equation 8 and equation 7 in equation 9:
by substituting equation 6
in equation 8 and equation 7 in equation 9:
Furthermore, we can re-arrange the system given by equations 10 and
11 by sum and difference of the equations:
So far, we have not assumed any relation between the vectors
characterizing the source and receiver planes, 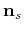 and
and
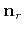 . However, if the source and receiver wavefields correspond to a
reflection from a planar interface, these vectors are not independent
of one-another, but are related by Snell's law which can be formulated
as
. However, if the source and receiver wavefields correspond to a
reflection from a planar interface, these vectors are not independent
of one-another, but are related by Snell's law which can be formulated
as
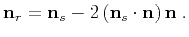 |
(14) |
This relations follows from geometrical considerations and it is based
on the conservation of ray vector projection along the
reflector. Equation 14 is only valid for PP reflections in an
isotropic medium.
Substituting Snell's law into the system 12-13,
and after trivial manipulations of the equations, we obtain the
system:
In general, the plane characterizing the source wavefield is not
orthogonal to the reflection plane (there would be no reflection in
that case), therefore we can simplify equation 16 by dropping the
term
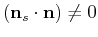 . Moreover, we can replace in equation 15
the expression in the square bracket with the quantity
. Moreover, we can replace in equation 15
the expression in the square bracket with the quantity
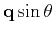 , where
, where 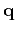 is the unit vector characterizing the
line at the intersection of the reflection and reflector planes, and
is the unit vector characterizing the
line at the intersection of the reflection and reflector planes, and
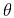 is the reflection angle contained in the reflection
plane. With these simplifications, the system
15-16 can be re-written as:
is the reflection angle contained in the reflection
plane. With these simplifications, the system
15-16 can be re-written as:
The system 17-18 allows for a straightforward
physical interpretation of the extended imaging condition. First, the
expression 18 indicates that of all possible space-lags that
can be applied to the reconstructed wavefields, the only ones that
contribute to the extended image are those for which the space-lag
vector
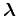 is orthogonal to the reflector normal vector
is orthogonal to the reflector normal vector
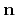 . Furthermore, assuming that the space-shift applied to the
source and receiver planes is contained in the reflector plane,
i.e.
. Furthermore, assuming that the space-shift applied to the
source and receiver planes is contained in the reflector plane,
i.e.
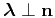 , then the expression 17 describe the
moveout function in an extended gather as a function of the space-lag
, then the expression 17 describe the
moveout function in an extended gather as a function of the space-lag
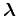 , the time lag
, the time lag 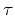 , the reflection angle
, the reflection angle 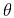 , the
orientation vector
, the
orientation vector 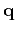 . The vector
. The vector 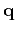 is orthogonal to the
reflector normal and depends on the reflection azimuth angle
is orthogonal to the
reflector normal and depends on the reflection azimuth angle 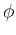 .
.
Figures 1-3 illustrate the process involved in the
extended imaging condition and describe pictorially its physical
meaning. Figure 1 shows the source and receiver planes, as well
as the reflector plane together with their unit vector
normals. Figure 2 shows the source and receiver planes
displaced by the space lag vector
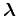 contained in the reflector
plane, as indicated by equation 18. The displaced planes do not
intersect at the reflection plane, thus they do not contribute to the
extended image at this point. However, with the application of time
shifts with the quantity
contained in the reflector
plane, as indicated by equation 18. The displaced planes do not
intersect at the reflection plane, thus they do not contribute to the
extended image at this point. However, with the application of time
shifts with the quantity
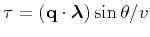 ,
i.e. a translation in the direction of plane normals, the source and
receiver planes are restored to the image point, thus contributing to
the extended image, Figure 3.
,
i.e. a translation in the direction of plane normals, the source and
receiver planes are restored to the image point, thus contributing to
the extended image, Figure 3.
|
|---|
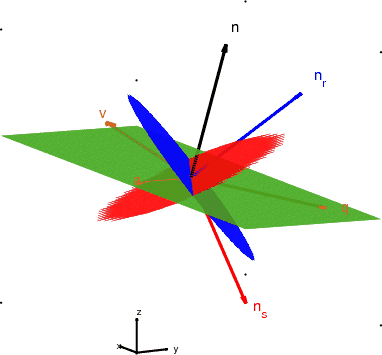
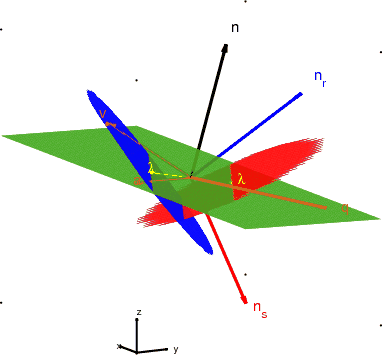
eicawfl
Figure 1. The reflector plane (of normal
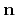 ), together with the source and receiver planes (of normals
), together with the source and receiver planes (of normals
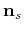 and
and 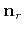 , respectively). The figure represents the
source/receiver planes in their original position, i.e. as obtained
by wavefield reconstruction.
, respectively). The figure represents the
source/receiver planes in their original position, i.e. as obtained
by wavefield reconstruction.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png)
|
|---|
|
|---|
eicxshift1
Figure 2. The reflector plane (of
normal 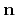 ), together with the source and receiver planes (of
normals
), together with the source and receiver planes (of
normals 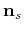 and
and 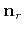 , respectively). The figure represents the
source/receiver planes displaced with the space-lag
, respectively). The figure represents the
source/receiver planes displaced with the space-lag
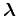 constrained in the reflector plane.
constrained in the reflector plane.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png)
|
|---|
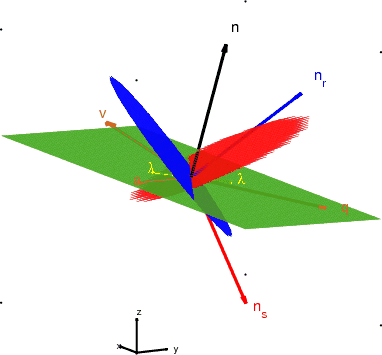
|
|---|
eictshift1
Figure 3. The reflector plane (of
normal 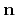 ), together with the source and receiver planes (of
normals
), together with the source and receiver planes (of
normals 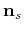 and
and 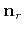 , respectively). The figure represents the
source/receiver planes displaced with space-lag
, respectively). The figure represents the
source/receiver planes displaced with space-lag
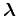 and time-lag
and time-lag
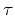 . The space and time-lags are related by equation 17.
. The space and time-lags are related by equation 17.
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png) ![[matlab]](icons/matlab.png)
|
|---|
 |
 |
 |
 | Wide-azimuth angle gathers for wave-equation migration |  |
![[pdf]](icons/pdf.png) |
Next: Angle decomposition
Up: Sava & Vlad: wide-azimuth
Previous: Imaging conditions
2013-08-29
![]() domain. The
purpose of this derivation is to find a procedure for angle
decomposition, i.e. a representation of reflectivity as a function of
reflection and azimuth angles.
domain. The
purpose of this derivation is to find a procedure for angle
decomposition, i.e. a representation of reflectivity as a function of
reflection and azimuth angles.
![]() by substituting equation 6
in equation 8 and equation 7 in equation 9:
by substituting equation 6
in equation 8 and equation 7 in equation 9:
![]() and
and
![]() . However, if the source and receiver wavefields correspond to a
reflection from a planar interface, these vectors are not independent
of one-another, but are related by Snell's law which can be formulated
as
. However, if the source and receiver wavefields correspond to a
reflection from a planar interface, these vectors are not independent
of one-another, but are related by Snell's law which can be formulated
as
![]() contained in the reflector
plane, as indicated by equation 18. The displaced planes do not
intersect at the reflection plane, thus they do not contribute to the
extended image at this point. However, with the application of time
shifts with the quantity
contained in the reflector
plane, as indicated by equation 18. The displaced planes do not
intersect at the reflection plane, thus they do not contribute to the
extended image at this point. However, with the application of time
shifts with the quantity
![]() ,
i.e. a translation in the direction of plane normals, the source and
receiver planes are restored to the image point, thus contributing to
the extended image, Figure 3.
,
i.e. a translation in the direction of plane normals, the source and
receiver planes are restored to the image point, thus contributing to
the extended image, Figure 3.


