|
|
|
|
Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |




|
|---|
|
elpf,delpf,sdip,median,dmedian
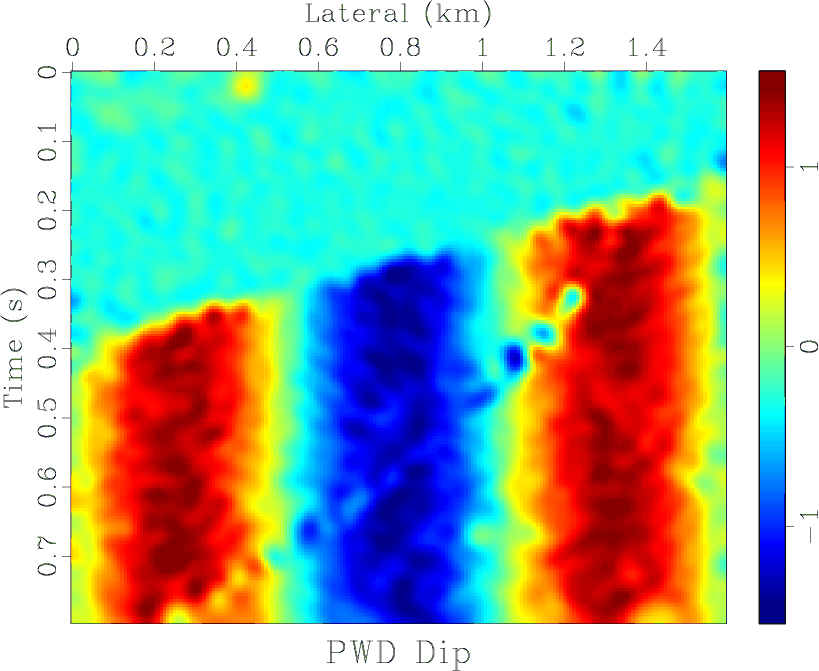
Figure 3. Analysis of results using different structure-oriented filtering. Nonstationary polynomial fitting (a), difference profile of nonstationary polynomial fitting (b), local PWD-based dip (c), median filter (d), and difference profile of median filter (e). |
|
|
We construct a new structure-oriented filtering method based on the 2D Hilbert transform with nonstationary polynomial fitting and apply it to synthetic data (Figure 1a). The local seismic dip (Figure 1d) controls the trend of the event, and we apply nonstationary polynomial fitting along the direction of the dip for fast structural interpretation using structure-oriented filtering. We achieve continuous model protection in the direction of dip, and noise attenuation and fault protection because of the use of nonstationary polynomial fitting. Nine sampling points are used in the structure-oriented filtering and five sampling points in the nonstationary polynomial fitting. The filtering results are shown in Figure 3a and the difference profile is shown in Figure 3b. Figure 3a shows that the upper tilted layer, the lower sinusoidal layer, and the fault information are preserved, while the noise is clearly suppressed. Random noise constitutes most of the difference profile without any tilted layer and fault information left because the local seismic dip cannot reflect the trend of the layers and owing to the attenuation of the limited effective information. To compare the proposed method with the PWD-based local dip estimation method (Figure 3c) with similar dip accuracy (Figure 1d), we choose the median filter and show the results in Figure 3d and the difference profile in Figure 3e. We compare the two profiles after the application of the median filter. We find more useful structural information than the method we proposed. That means the method we proposed has better effect.
|
|
|
|
Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |