Applications of plane-wave destruction filters

Bibliography

Abma, R., and J. Claerbout, 1995, Lateral prediction for noise attenuation by t-x and F-X techniques: Geophysics, 60, 1887-1896.

Bednar, J. B., 1998, Least squares dip and coherency attributes: 68th Ann. Internat. Mtg, Soc. of Expl. Geophys., 653-655.

Brown, M., and R. Clapp, 2000, T-X domain, pattern-based ground-roll removal, in 70th Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts: Soc. Expl. Geophys., 2103-2106.

Burg, J. P., 1975, Maximum entropy spectral analysis: PhD thesis, Stanford University.

Canales, L. L., 1984, Random noise reduction: 54th Ann. Internat. Mtg, Soc. of Expl. Geophys., Session:S10.1.

Claerbout, J., 1998, Multidimensional recursive filters via a helix: Geophysics, 63, 1532-1541.

----, 1999, Geophysical estimation by example: Environmental soundin gs image enhancement: Stanford Exploration Project.

Claerbout, J., and M. Brown, 1999, Two-dimensional textures and prediction-error filters: 61st Mtg., Eur. Assn. Geosci. Eng., Session:1009.

Claerbout, J. F., 1992, Earth Soundings Analysis: Processing Versus Inversion: Blackwell Scientific Publications.

----, 1994, Applications of two- and three-dimensional filtering: 64th Ann. Internat. Mtg, Soc. of Expl. Geophys., 1572-1575.

Clapp, R. G., 2001, Geologically constrained migration velocity analysis: PhD thesis, Stanford University.

Clapp, R. G., B. L. Biondi, S. B. Fomel, and J. F. Claerbout, 1998, Regularizing velocity estimation using geologic dip information: 68th Ann. Internat. Mtg, Soc. of Expl. Geophys., 1851-1854.

Crawley, S., 2000, Seismic trace interpolation with nonstationary prediction-error filters: PhD thesis, Stanford University.

Crawley, S., J. Claerbout, and R. Clapp, 1999, Interpolation with smoothly nonstationary prediction-error filters: 69th Ann. Internat. Mtg, Soc. of Expl. Geophys., 1154-1157.

Fomel, S., 2001, Three-dimensional seismic data regularization: PhD thesis, Stanford University.

Fomel, S., and J. F. Claerbout, 2002, Multidimensional recursive filter preconditioning in geophysical estimation problems: Geophysics, accepted for publication.

Freeman, W. T., and E. H. Adelson, 1991, The design and use of steerable filters: IEEE Trans. on Pattern Analysis and Machine Intelligence, 1, 891-906.

Guitton, A., M. Brown, J. Rickett, and R. Clapp, 2001, Multiple attenuation using a t-x pattern-based subtraction method: 71st Ann. Internat. Mtg, Soc. of Expl. Geophys., 1305-1308.

Gulunay, N., 1986, Fx decon and complex Wiener prediction filter: 56th Ann. Internat. Mtg., Soc. of Expl. Geophys., Session:POS2.10.

Harlan, W. S., J. F. Claerbout, and F. Rocca, 1984, Signal/noise separation and velocity estimation: Geophysics, 49, 1869-1880.

Kim, S., and W. W. Symes, 1998, Smooth detectors of linear phase: Inverse Problems, 14, 101-112.

Neidell, N. S., and M. T. Taner, 1971, Semblance and other coherency measures for multichannel data: Geophysics, 36, 482-497.

Nichols, D., 1990, Estimation of missing data by least squares, in SEP-65: Stanford Exploration Project, 271-294.

Schwab, M., 1998, Enhancement of discontinuities in seismic 3-D images using a Java estimation library: PhD thesis, Stanford University.

Schwab, M., J. Claerbout, and C. Holden, 1996, Revealing geological discontinuities by plane reflector suppression, in 66th Annual Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts: Society Of Exploration Geophysicists, 302-305.

Simoncelli, E. P., and H. Farid, 1996, Steerable wedge filters for local orientation analysis: IEEE Trans. on Image Processing, 5, 1377-1382.

Soubaras, R., 1995, Prestack random and impulsive noise attenuation by F-X projection filtering: 65th Ann. Internat. Mtg, Soc. of Expl. Geophys., 711-714.

Spitz, S., 1991, Seismic trace interpolation in the F-X domain: Geophysics, 56, 785-794.

----, 1999, Pattern recognition, spatial predictability, and subtraction of multiple events: The Leading Edge, 18, 55-58.

Symes, W. W., 1994, The plane wave detection problem: Inverse Problems, 10, 1361-1391.

Symes, W. W., and J. J. Carazzone, 1991, Velocity inversion by differential semblance optimization: Geophysics, 56, 654-663.

Yilmaz, O., and D. Cumro, 1983, Worldwide assortment of field seismic records, released by Western Geophysical Company of America: Houston.

Appendix A

Determining filter coefficients by Taylor expansion

This appendix details the derivation of equations (9) and (10). The main idea to match the frequency responses of the approximate plane-wave filters to the response of the exact phase-shift operator at low frequencies.

The Taylor series expansion of the phase-shift operator 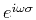$e^{i \omega \sigma}$ around the zero frequency 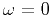$\omega=0$ takes the form

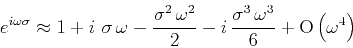$$e^{i \omega \sigma} \approx 1 + i\, \,\sigma\,\omega - \f... ...frac{\sigma^3\,\omega^3}{6} + \mbox{O}\left(\omega^4\right)$$ (24)

The Taylor expansion of the six-point implicit finite-difference operator takes the form

$$\frac{B_3(Z_t)}{B_3(1/Z_t)} = \frac {b_{-1}\,Z_t^{-1} + b_0 + b_1\,Z_t} {b_1\,Z_t + b_0 + b_{-1... ...a} + b_0 + b_1\,e^{i \omega}} {b_1\,e^{-i \omega} + b_0 + b_{-1}\,e^{i \omega}}$$

$$\approx 1 - \frac{2\,i \,\left( b_{-1} - b_1 \right) \,\omega}{b_0 + b_{-... ...\left( b_{-1} - b_1 \right)^2\,\omega^2} {\left( b_0 + b_{-1} + b_1 \right)^2}$$

$$+ \frac{i\, \left( b_{-1} - b_1 \right) \, \left[ b_0^2 - b_0... ...^2 \right) \right] \,\omega^3} {3\,\left(b_0 + b_{-1} + b_1\right)^3} + \ldots$$ (25)

Matching the corresponding terms of expansions (A-1) and (A-2), we arrive at the system of nonlinear equations

$$\sigma = \frac{2\,\left( b_1 - b_{-1} \right) } {b_0 + b_{-1} +b_1}$$ (26)

$$\sigma^2 = \frac{4\,\left( b_1 - b_{-1} \right)^2} {\left(b_0 + b_{-1} +b_1 \right)^2}$$ (27)

$$\sigma^3 = \frac{2\,\left( b_1 - b_{-1} \right) \, \left[ b_0^2 - b_0\,\lef... ...\,b_{-1}\,b_1 + b_1^2 \right) \right] } {\left(b_0 + b_{-1} + b_1 \right)^3}$$ (28)

System (A-3-A-5) does not uniquely constrain the filter coefficients 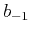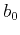$b_{-1}$, $b_0$, and $b_1$ because equation (A-4) simply follows from (A-3) andb ecause all the coefficients can be multiplied simultaneously by an arbitrary constant without affecting the ratios in equation (A-2). I chose an additional constraint in the form

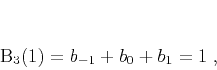$$B_3(1) = b_{-1} + b_0 + b_1 = 1\;,$$ (29)

which ensures that the filter 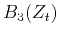$B_3(Z_t)$ does not alter the zero frequency component. System (A-3-A-5) with the additional constraint (A-6) resolves uniquely to the coefficients of filter (9) in the main text:

$$b_{-1} = \frac{(1-\sigma)(2-\sigma)}{12}\;;$$ (30)

$$b_0 = \frac{(2+\sigma)(2-\sigma)}{6}\;;$$ (31)

$$b_1 = \frac{(1+\sigma)(2+\sigma)}{12}\;.$$ (32)

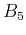The $B_5$ filter of equation (10) is constructed in a completely analogous way, using longer Taylor expansions to constrain the additional coefficients. Generalization to longer filters is straightforward.

The technique of this appendix aims at matching the filter responses at low frequencies. One might construct different filter families by employing other criteria for filter design (least squares fit, equiripple, etc.)

Applications of plane-wave destruction filters